Regnemaskine for Pythagoras sætning
Beregn sidelængderne eller arealet af en retvinklet trekant ved hjælp af Pythagoras sætning.
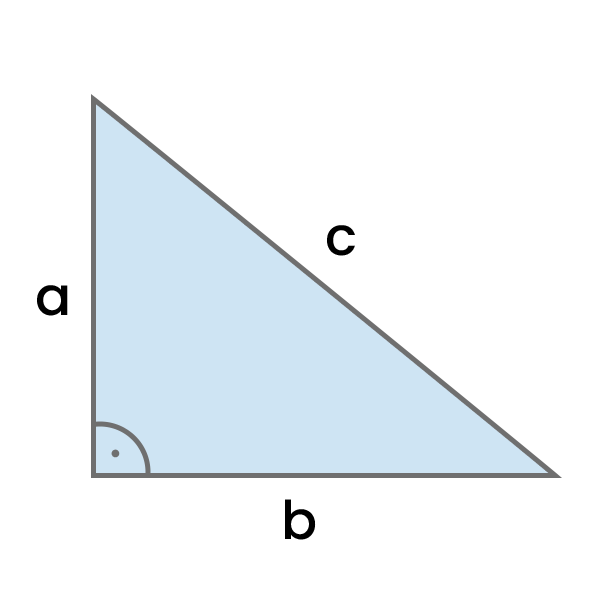
Indtast længderne af hver side af den retvinklede trekant, bestem enheden og beregn længderne af de andre sider og trekantens areal. Ud over resultaterne viser lommeregneren også den detaljerede proces med at beregne længden af en given side og trekantens areal.
Beregningsformel
- a = Sidelængde (a)
- b = Sidelængde (b)
- c = Længden af hypotenusen (c)
For at finde længden af side a, udregn kvadratroden ved at trække længden af hypotenusen c i anden kvadrat og længden af side b i anden.
$$ a = \sqrt{c^{2} - b^{2}} $$For at finde længden af side b skal du beregne kvadratroden ved at trække længden af hypotenusen c i anden potens og længden af side a i anden.
$$ b = \sqrt{c^{2} - a^{2}} $$For at beregne længden af hypotenusen c skal du beregne kvadratroden af resultatet af at lægge længden af side a til kvadratet og længden af side b til kvadratet.
$$ c = \sqrt{a^{2} + b^{2}} $$For at finde arealet af en retvinklet trekant skal du dividere resultatet af at gange side a og b med 2.
$$ A = \dfrac {ab}{2} $$